A simple yet effective approach for turning a polarization camera into a snapshot HDR camera.

This project was selected for a poster and demo at ICCP 2023.

Abstract

High dynamic range (HDR) images are important for a range of tasks, from navigation to consumer photography. Accordingly, a host of specialized HDR sensors have been developed, the most successful of which are based on capturing variable per-pixel exposures. In essence, these methods capture an entire exposure bracket sequence at once in a single shot. This paper presents a straightforward but highly effective approach for turning an off-the-shelf polarization camera into a high-performance HDR camera. By placing a linear polarizer in front of the polarization camera, we are able to simultaneously capture four images with varied exposures, which are determined by the orientation of the polarizer. We develop an outlier-robust and self-calibrating algorithm to reconstruct an HDR image (at a single polarity) from these measurements. Finally, we demonstrate the efficacy of our approach with extensive real-world experiments.

Method

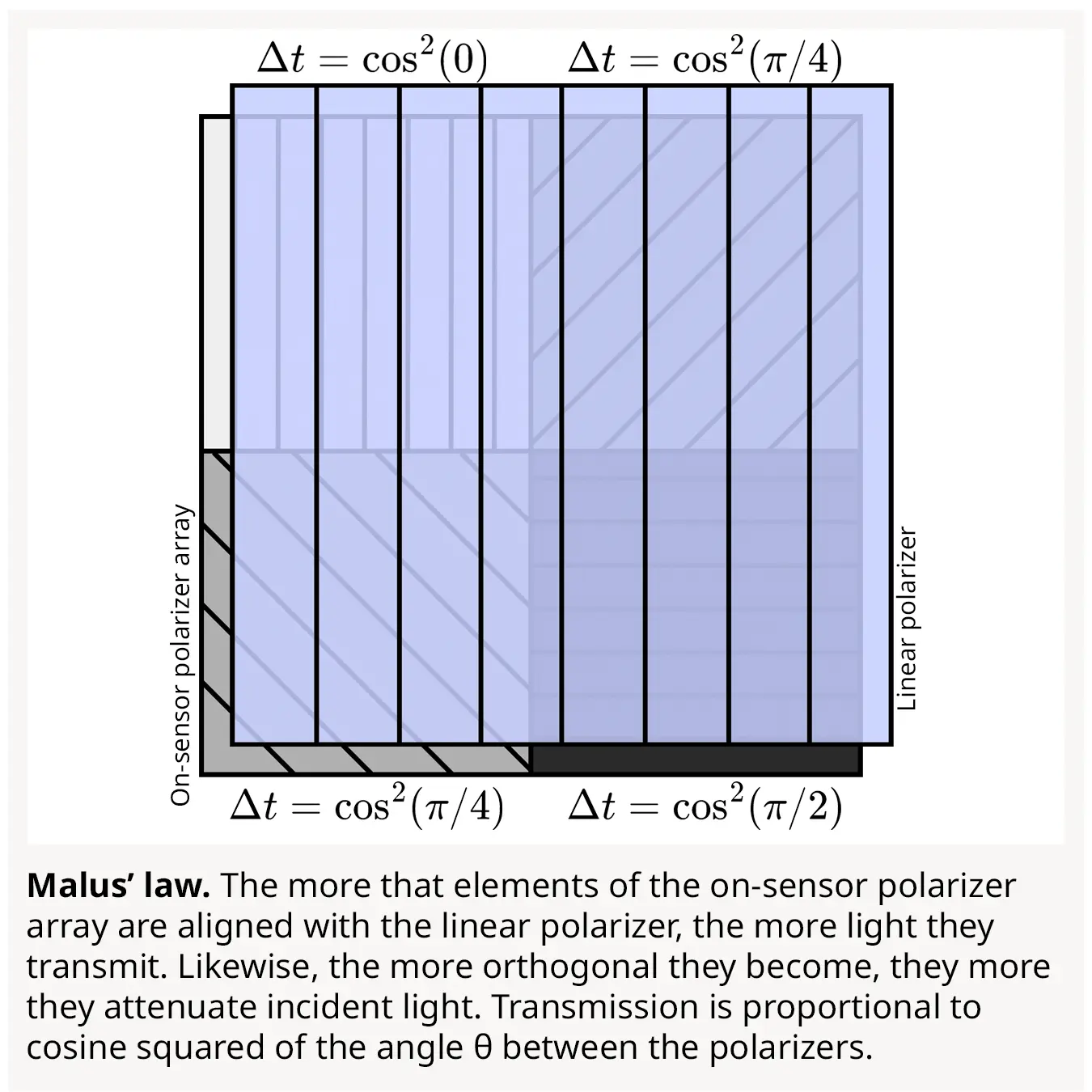
The intensity of light observed through two polarizers \(I\) is linearly dependent on the cosine squared of the angle \(\theta\) between the polarizers. In other words, as the polarizers’ angles become more orthogonal, they transmit less of the incident light \(I_0\) (and vice-versa).

\[I(\theta) = I_0\text{cos}^2(\theta)\]

Placing an additional polarizer in front of the lens of our polarization camera, we simultaneously capture a set of four images \(S=\{I(\theta_1), I(\theta_2), I(\theta_3), I(\theta_4)\}\) corresponding to polarization angles \(\{0, \frac{\pi}{4}, \frac{\pi}{2}, \frac{3\pi}{4}\}\) respectively. Each image has a transmission rate dependent on \(\theta\) that determines their exposure time.

We estimate the exposure time of each image \(I(\theta_i)\) by observing that pixels in the on-sensor polarizer array share the following relationships:

\[\theta_3 = \theta_1 + \frac{\pi}{2}\] \[\theta_4 = \theta_2 + \frac{\pi}{2}\]

Using Malus’ law, we can express images \(I(\theta_1)\) and \(I(\theta_3)\) in terms of \(\theta_1\):

\[I(\theta_1) = I_0\text{cos}^2\theta_1\] \[I(\theta_3) = I_0\text{sin}^2\theta_1\]

Combining these two, we obtain a closed-form solution for estimating angle \(\theta_1\)

\[\hat{\theta}_1 = \text{arctan}\left(\sqrt{\frac{I(\theta_3)}{I(\theta_1)}}\right)\]

and plug it into Malus’ law to obtain an estimate of exposure time \(\text{cos}^2(\hat{\theta}_1)\). For brevity, we omit closed-form solutions for \(\hat{\theta}_2, \hat{\theta}_3, \hat{\theta}_4\) as their derivations follow the same structure as our derivation for \(\hat{\theta}_1\).

It is important to note that angle estimates \(\hat{\theta}\) are computed over for \(P\) pixels of the image. We aggregate these estimates by taking their mode to obtain our final (scalar) estimate

\[\hat{\theta}_{i} = \text{Mode}(\hat{\theta}_{i,j}), j \in [1, P].\]

After estimating exposure times for all four images, we merge the images together using a weighted average to form an HDR image

\[H = \frac{1}{N}\sum^N_i \frac{I(\theta_i)}{\text{cos}^2(\hat{\theta}_i)}\]

Results

We reconstruct HDR images of a diverse set of natural scenes from snapshots taken with a polarization camera.